Dart: Trie Data Structure: The Key to Fast and Effective Search

Structure

Trie (same pronunciation as “try”) is a tree-like data structure. It has the following looks. Let’s assume that we have only alphabets, a to z.

Each node has nodes a to z
A node that has an end of a word is called KeyNode

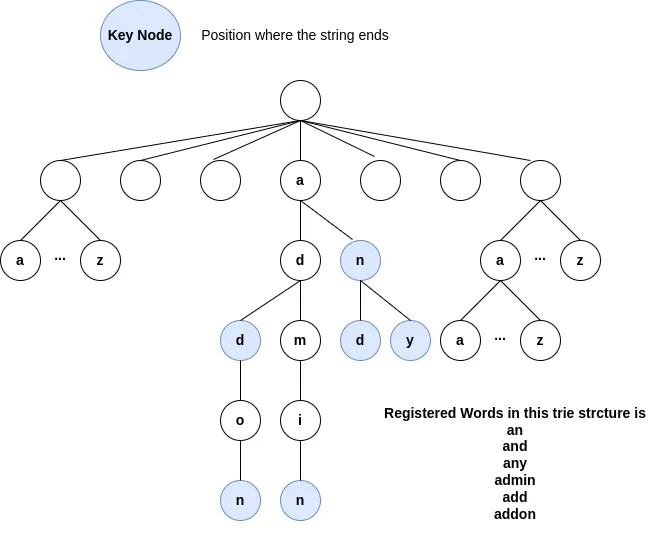
In this example, we add the following words.

an
and
any
admin
add
addon

Some words have the same letters in the string. Therefore, they can use the same node to store the info.

Trie can reduce memory usage when many words have overlaps.

Advantages and Disadvantages

Here are some advantages and disadvantages of trie data structures. While tries offer advantages like efficient prefix searches and space efficiency, they also have drawbacks such as high space complexity and potential memory consumption at the same time. The choice to use a trie depends on the specific requirements of the application and the characteristics of the data being stored.

Advantages

Prefix Search
Tries are particularly efficient for prefix searches, making them suitable for tasks like autocomplete or dictionary implementations. Retrieving all keys with a common prefix is quick and requires minimal comparisons.
Space Efficiency
Tries can be more space-efficient compared to other data structures, especially when there is a significant amount of overlap among the keys. Common prefixes are shared among different keys, reducing redundancy.
Insertion and Deletion
Inserting and deleting keys in a trie can be efficient. It generally takes O(m) time complexity, where m is the length of the key.
Ordered Output
Tries naturally provide an ordered representation of the keys, making it easy to traverse the keys in lexicographical order.
No Collision Issues
Unlike hash tables, tries do not suffer from collisions since each node in the trie represents a distinct character in the key.

Disadvantages

Space Complexity
Tries can have high space overhead, especially when dealing with large alphabets or long keys. Each node in the trie represents a character, which can lead to a large number of nodes.
Memory Consumption
Tries can be memory-intensive, especially when storing a large number of short keys, as each character in the key requires a separate node.
Complex Implementation
Implementing a trie can be more complex compared to other data structures like hash tables or binary search trees.
Not Well-suited for Numeric Keys
Tries are primarily designed for keys that are sequences of characters, such as strings. They may not be the most efficient choice for numeric keys.
Cache Inefficiency
Tries may not exploit cache locality as effectively as some other data structures, which could impact performance in certain scenarios.

Applications to use trie data structure

It’s better to know in which technologies the data structure is applied so that we can apply it to our applications.

Text Editors and Autocomplete
Tries are frequently used in text editors and applications that provide autocomplete suggestions. The efficient prefix search capabilities of tries make them well-suited for quickly retrieving and suggesting words as user types.
Spell Checkers
Tries are utilized in spell checkers to efficiently identify misspelled words or suggest corrections. The ordered nature of tries facilitates the quick identification of potential corrections based on similar prefixes.
IP Routing
Tries are employed in networking and IP routing algorithms to store and look up routing information efficiently. IP addresses can be represented as sequences of numbers and tries allow for quick matching and retrieval of routing information.
Symbol Tables
Tries are used as symbol tables in compilers and interpreters. They facilitate efficient storage and retrieval of variable names, keywords, or identifiers during the compilation or interpretation process.
Distributed Systems
In distributed systems, tries can be employed for consistent hashing. The ordered nature of tries allows for the efficient distribution of keys across nodes in a distributed environment.
Caching Systems
Tries can be used in caching systems to represent hierarchical cache structures. This enables efficient lookup and management of cached data based on hierarchical keys.
Network Routing Tables
Tries are used in the representation of routing tables in routers and switches. The hierarchical structure allows for quick and efficient lookup of destination addresses in network routing.
Genetic Databases
Tries can be employed in genetic databases to efficiently store and retrieve DNA sequences. The hierarchical nature of tries is suitable for representing the structure of genetic sequences.
Natural Language Processing
Tries are used in natural language processing tasks, such as language modeling and text analysis. They facilitate quick searches for words or phrases in a corpus.
Compression Algorithms
Tries can be utilized in compression algorithms, such as Huffman coding. They provide an efficient way to represent and compress variable-length codes.

Implementation

Trie Node

We need to define TrieNode which is used to represent a character and to determine if the node is the end of a word.

import 'dart:collection';

class TrieNode {
  bool isKeyNode = false;
  final HashMap<String, TrieNode?> children = HashMap();
}

If isKeyNode is true, it means that the node is end of a word.

Then, We also define Trie class that implements the main features.

import 'package:dart/trie/trie_node.dart';

class Trie {
  TrieNode root = TrieNode();
}

Trie has only one node at first.

Insert

The first one is insert. When we want to add “and”, each letter must be registered. Each node has a representation of a letter. Therefore, if the letter has not been registered, the node needs to be added. The process is done in addNewBranch().

void insert(String s) {
  if (s.isEmpty) {
    return;
  }

  TrieNode currentNode = root;
  for (int i = 0; i < s.length; i++) {
    final c = s[i];

    final child = currentNode.children[c];
    if (child == null) {
      addNewBranch(currentNode, s.substring(i));

      return;
    }

    currentNode = child;
  }

  currentNode.isKeyNode = true;
}

Don’t forget to set true to isKeyNode at the end node.

Let’s see the implementation of addNewBranch(). Each character has to add a new node. Then, set true to isKeyNode.

void addNewBranch(TrieNode node, String s) {
  TrieNode currentNode = node;
  for (int i = 0; i < s.length; i++) {
    final newNode = TrieNode();
    currentNode.children[s[i]] = newNode;
    currentNode = newNode;
  }

  currentNode.isKeyNode = true;
}

Search

Next is search method. It tries to find the last character of the specified word. Therefore, it loops over the string and traverses the node tree. It’s easy.

TrieNode? search(String s) {
  if (s.isEmpty) {
    return null;
  }

  TrieNode result = root;
  for (int i = 0; i < s.length; i++) {
    final child = result.children[s[i]];
    if (child == null) {
      return null;
    }

    result = child;
  }

  return result;
}

Remove

If we want to remove a word, search it and set false to isKeyNode at the end node.

bool remove(String s) {
  final foundNode = search(s);
  if (foundNode == null || !foundNode.isKeyNode) {
    return false;
  }

  foundNode.isKeyNode = false;
  return true;
}

The logic is simple but it doesn’t remove the node itself which leads to storing unnecessary memory.

bool prune(String s) {
  final (deleted, _) = _prune(root, s);

  return deleted;
}

(bool, bool) _prune(TrieNode node, String s) {
  if (s.isEmpty) {
    final deleted = node.isKeyNode;
    node.isKeyNode = false;

    return (deleted, node.children.isEmpty);
  }

  final child = node.children[s[0]];
  if (child != null) {
    var (deleted, shouldPrune) = _prune(child, s.substring(1));
    if (deleted && shouldPrune) {
      node.children.remove(s[0]);
      if (node.isKeyNode || node.children.isNotEmpty) {
        shouldPrune = false;
      }
    }
    return (deleted, shouldPrune);
  }

  return (false, false); // key not found
}

The first if clause handles the end node. The middle part traverses the node to the end node by recursive call. Then, remove the key-value pair if the node is no longer used. Of course, the node must neither be a key node nor have a child.

Longest Prefix

We can get the longest prefix against the input string. This feature might not often used but it’s sometimes useful.

String? longestPrefix(String s) {
  return _longestPrefix(root, s, "");
}

String? _longestPrefix(TrieNode node, String s, prefix) {
  if (s.isEmpty) {
    if (node.isKeyNode) {
      return prefix;
    }

    return null; // key not found
  }

  final c = s[0];
  final child = node.children[c];
  if (child == null) {
    if (node.isKeyNode) {
      return prefix;
    }

    return null; // key not found
  }

  final result = _longestPrefix(child, s.substring(1), prefix + c);
  if (result != null) {
    return result;
  } else if (node.isKeyNode) {
    return prefix;
  }

  return null; // key not found
}

This is not complicated. There are 3 cases.

The search string is empty (it’s an end node)
Node doesn’t find for the key
Node has a child

When a node has a child, it calls the function again to step in the next child node.

startWith

It’s helpful if the search result shows candidates of the words when a user inputs half of a word. We often see this feature when we search for something on search engines.

List<String> startWith(String prefix) {
  final node = search(prefix);
  if (node == null) {
    return [];
  }

  return _startWith(node, prefix);
}

List<String> _startWith(TrieNode node, String prefix) {
  final List<String> result = [];
  if (node.isKeyNode) {
    result.add(prefix);
  }

  for (final child in node.children.entries) {
    result.addAll(_startWith(child.value, prefix + child.key));
  }

  return result;
}

The first thing to do is to find the end node of the prefix. If the prefix doesn’t exist in the tree, we can’t show any candidates.

If the target key is a key node, it’s a word that we can show. Therefore, it must be added to the result.

Then, it traverses all the children to find key nodes and add them. It’s simple logic.

Execution Result

We have implemented the necessary features, so we can now try to use them.

import 'package:dart/trie/trie.dart';

String check(Trie trie, String str) {
  final node = trie.search(str);

  if (node == null) {
    return "node not found";
  }

  return node.isKeyNode ? "Key node" : "not a key node";
}

void main(List<String> args) {
  final trie = Trie();
  trie.insert("and");
  trie.insert("an");
  trie.insert("answer");
  trie.insert("ankle");
  trie.insert("android");
  trie.insert("an and");

  print("---search---");
  print(check(trie, "an")); // Key node
  print(check(trie, "and")); // Key node
  print(check(trie, "answer")); // Key node
  print(check(trie, "ankle")); // Key node
  print(check(trie, "android")); // Key node
  print(check(trie, "a")); // not a key node

  print("---longest prefix---");
  print(trie.longestPrefix("answering")); // answer
  print(trie.longestPrefix("android")); // android

  print("---startWith---");
  print(trie.startWith("and")); // [and, android]
  print(trie.startWith("unknown")); // []

  print("---remove/prune---");
  print(trie.prune("android")); // true
  print(trie.remove("unknown_word")); // false

  print(trie.longestPrefix("android")); // and  
}

It looks working well. The key “android” is removed. Therefore longestPrefix() returns a different result before and after the removal.

Data structure based on Trie

The basic trie structure can be extended or modified in various ways to enhance its functionality or address specific requirements. Here are some variations or data structures based on the trie that can be used to improve certain aspects.

Compressed Trie (Radix Trie)
In a compressed trie, common branches with a single child are compressed into a single node. This helps reduce the overall space complexity of the trie, making it more memory-efficient. It’s particularly useful when there are many nodes with only one child.
Ternary Search Trie (TST)
Ternary Search Tries are an improvement over standard tries, where each node has three children (less than, equal to, and greater than). TSTs are often used in spell checkers and dictionary implementations, providing a good balance between space efficiency and search performance.
Suffix Trie (or Suffix Tree)
A suffix trie is a specialized trie used for storing all the suffixes of a given text or set of strings. Suffix tries are widely used in applications such as bioinformatics for pattern matching and indexing DNA sequences.
Double-Array Trie (DAT)
Double-Array Tries are a space-efficient implementation of tries, where two arrays are used to represent the transitions and output values. This structure minimizes memory consumption while maintaining quick access times, making it useful in memory-constrained environments.
Hash Trie
In a hash trie, instead of having an array of child nodes indexed by characters, a hash table is used. This can help mitigate some of the space inefficiencies of standard tries, especially when dealing with large character sets.
Multiway Trie (R-Way Trie)
In a multiway trie, each node can have more than two children. This is a generalization of the binary trie and allows for greater flexibility. The number of children per node is determined by the size of the alphabet or the radix of the trie.
Double-Hashed Trie
This is an extension of the hash trie where two hash functions are used for hashing, helping to reduce the chances of collisions in the hash table.
PATRICIA Trie
PATRICIA (Practical Algorithm to Retrieve Information Coded in Alphanumeric) is a compressed trie where each inner node with only one child is merged with its parent. This reduces memory consumption and enhances efficiency.
Multi-Key Trie
A multi-key trie is designed to store multiple keys in a single trie structure. This can be useful in scenarios where multiple related sets of keys need to be efficiently managed.
Burrows-Wheeler Trie
Used in compression algorithms like Burrows-Wheeler Transform, this trie variant represents the relationships between characters in the transformed text, facilitating efficient compression and decompression.

These variations on the trie data structure cater to different needs and trade-offs, addressing issues such as space efficiency, search speed, and adaptability to specific types of data. The choice of a particular trie variant depends on the specific requirements of the application.