I implemented Disjoint-Set in Dart as known as Union Find.
This post is the output of this book.
Advanced Algorithms and Data StructuresYou can check the completed code in my GitHub repository.
What is Disjoint-set used for?
Disjoint-set is used for grouping for multiple things. Assume that we have a lot of products in our online shop. Users can buy what they want. When users choose an item, we want to show some other products that are often bought together with it. If it is often bought together, the recommended items could also be useful for the users.
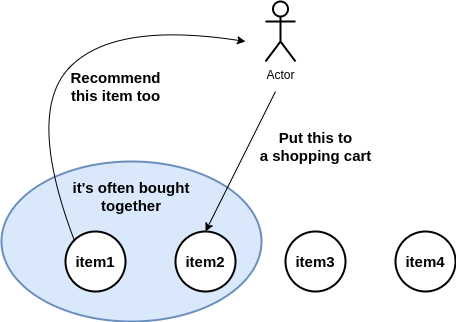
Disjoint-set answers whether the item belongs to the same group or not. It just manages the grouping as a structure and it doesn’t offer a way for the grouping logic. The logic needs to be considered separately.
It can answer in O(log(N)) time, so if you face a performance problem, it’s a good thing to learn.
Interface for Disjoint-set
Let’s look at the interface first. It has only 4 methods.
import 'dart:collection';
import 'package:dart/disjoint_sets/tree.dart';
typedef Element = int;
abstract class DisjointSetBase<T> {
HashMap<Element, T> partitionsMap = HashMap();
DisjointSetBase({HashMap<Element, T>? initialSet}) {
if (initialSet != null) {
partitionsMap = initialSet;
}
}
/// Add the specified element to the Disjoint set
bool add(Element elem);
/// Find the partition to which the specified element belongs.
T findPartition(Element elem);
/// Return true if the two objects belong to the same partition.
/// Otherwise false.
bool areDisjoint(Element elem1, Element elem2);
/// Merge the two elements into one group.
bool merge(Element elem1, Element elem2);
/// Show all elements in this Disjoint set.
void show() {
for (final key in partitionsMap.keys) {
print("$key: ${partitionsMap[key]}");
}
}
}- add: after the initialization, data must be added to it.
- findPartition: It finds the partition to which the item belongs. In other words, it finds a group for the item.
- areDisjoint: It checks whether the two items are in the same group or not.
- merge: Merge the two items.
show method is just a utility method to show the current state.
I use HashMap as a data type. It’s ok to use List instead if the number of items is small. However, if it needs to handle a large number of items, HashMap is faster. Reading a data from List is O(N) but O(1) from HashMap. Since reading operation is more often than adding an item, using HashMap here is reasonable.
I defined Element as integer type. If we need another data type or object, we can change the declaration. If it’s Object type, we need to define how to compare the two objects for == operation.
Check the following post, if you don’t know what to do.
Naive Solution with Set/List data type
The first implementation that we can easily come up with is using Set/List data type to group items.
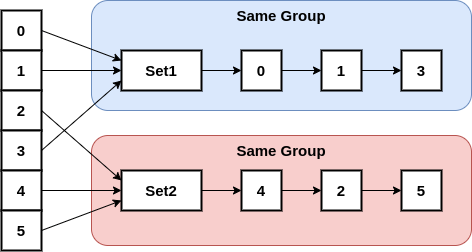
We will implement the following methods one by one. The value is Set<Element>.
class NaiveDisjointSet extends DisjointSetBase<Set<Element>> {
NaiveDisjointSet({HashMap<Element, Set<Element>>? initialSet})
: super(initialSet: initialSet);
@override
bool add(Element elem) { }
@override
Set<Element> findPartition(Element elem) { }
@override
bool areDisjoint(Element elem1, Element elem2) { }
@override
bool merge(Element elem1, Element elem2) { }
}Add
Let’s start with Add. It’s super simple, isn’t it?
@override
bool add(Element elem) {
if (partitionsMap.containsKey(elem)) {
return false;
}
partitionsMap[elem] = {elem};
return true;
}It returns true if the element doesn’t exist. Otherwise, false. It just creates a new group that contains only one element.
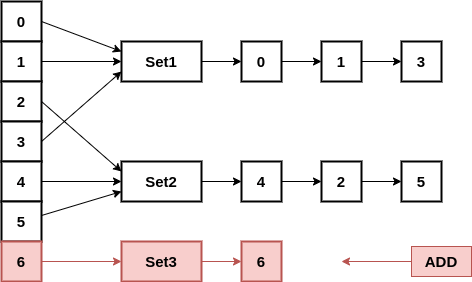
findPartition
No question about this method. Each key in the HashMap has a pointer to a group. It just returns the object here.
@override
Set<Element> findPartition(Element elem) {
if (!partitionsMap.containsKey(elem)) {
throw Exception("The element is not found. [$elem]");
}
return partitionsMap[elem]!;
}areDisjoint
This is the main method that the Disjoint-set wants to provide. It returns true if the two elements are in a different group.
@override
bool areDisjoint(Element elem1, Element elem2) {
return findPartition(elem1) != findPartition(elem2);
}merge
Merge logic is a little bit more complex but it’s easy. It does nothing if the two elements are already in the same group. If they are in a different group, an element in a group is added to another group one after another.
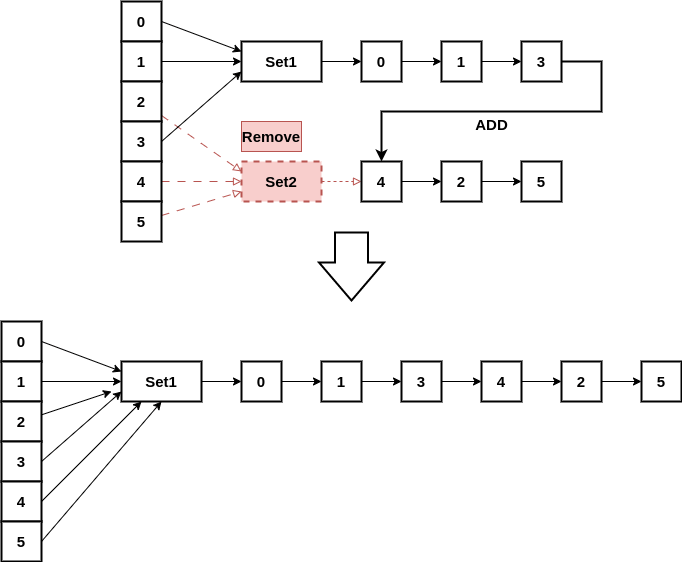
@override
bool merge(Element elem1, Element elem2) {
final p1 = findPartition(elem1);
final p2 = findPartition(elem2);
if (p1 == p2) {
return false;
}
for (final elem in p1) {
p2.add(elem);
partitionsMap[elem] = p2;
}
return true;
}Check the execution result
Let’s check the execution result here. The execution code is as follows.
void main(List<String> args) {
final naiveDisjointSet = NaiveDisjointSet();
run(naiveDisjointSet);
}
void run(DisjointSetBase disjointSet) {
disjointSet.add(1);
disjointSet.add(1);
disjointSet.add(2);
disjointSet.add(4);
disjointSet.add(5);
disjointSet.add(6);
disjointSet.add(7);
print("---current disjoint set---");
disjointSet.show();
// 1: {1}
// 2: {2}
// 4: {4}
// 5: {5}
// 6: {6}
// 7: {7}
print(disjointSet.findPartition(1)); // {1}
print(disjointSet.findPartition(4)); // {4}
print(disjointSet.areDisjoint(1, 4)); // true
print(disjointSet.merge(1, 4)); // true
print(disjointSet.areDisjoint(1, 4)); // false
print("---current disjoint set---");
disjointSet.show();
// 1: {4, 1}
// 2: {2}
// 4: {4, 1}
// 5: {5}
// 6: {6}
// 7: {7}
}Item 1 and 4 are merged in the example above. Therefore, both key 1 and 4 show the same result.
If the number of items is small enough, this implementation is okay. However, the more number of items increases, the more slowly the application becomes. We will improve the performance to address the case.
Tree like structured Disjoint-set
The problem in the previous solution is that the reading operation for List/Set is O(N). The bigger the data size becomes, the more time it takes to read the data.
To make it faster, make it into a Tree structure. Then, the read operation becomes O(log(N)). The bigger the size is, the faster the operation can be done than List/Set.
The tree structure is normally faster than an array, but it becomes the same as an array in the worst case. Look at the following image. We should avoid the tree becoming like an array.
Check the following post if you want to learn about tree structure.
Introduce an object
To represent the tree like structure, we need to define an object that has a link to a parent. It looks as follows.
class Tree {
Element root;
int rank;
Tree(this.root, {this.rank = 1});
@override
String toString() {
return "{ root: $root, rank: $rank }";
}
}I used the same term rank used in the book but I think size is a better choice. It represents the number of items in the tree.
The value of the HashMap changes to Tree instead of Set<Element>.
class TreeDisJointSet extends DisjointSetBase<Tree> {
TreeDisJointSet({HashMap<Element, Tree>? initialSet})
: super(initialSet: initialSet);Improve merge method
We need to create a tree structure when the two items are merged. So we need to improve merge method in the following way.
@override
bool merge(Element elem1, Element elem2) {
final p1 = findPartition(elem1);
final p2 = findPartition(elem2);
if (p1.root == p2.root) {
return false;
}
if (p1.rank >= p2.rank) {
p2.root = p1.root;
p1.rank += p2.rank;
} else {
p1.root = p2.root;
p2.rank += p1.rank;
}
return true;
}The main part of this method is if-else statement. We want to avoid the tree becoming linear. The smaller tree becomes the subtree of the other tree here. If there is no such condition, it could become linear.
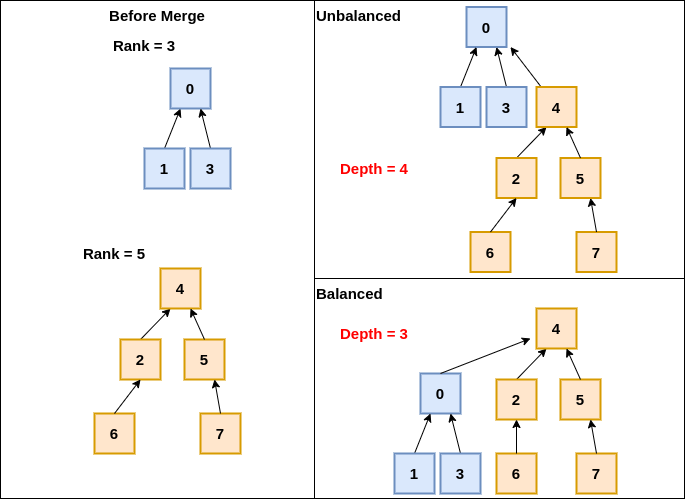
As shown in the image, each value has a pointer to the parent.
Improve findPartition
We updated the structure. Therefore, we need to update findPartition method too.
As we saw in the image above, we can reach the root of the tree if we go up through each parent. We have to implement it. The code becomes as follows.
@override
Tree findPartition(Element elem) {
if (!partitionsMap.containsKey(elem)) {
throw Exception("The element is not found. [$elem]");
}
var current = partitionsMap[elem]!;
if (current.root != elem) {
// Go to the root of the Tree
current = findPartition(current.root);
}
return current;
}The root property of the root element has the same value as the element. If the value is different, it’s on the way to root and thus call findPartition recursively. It returns the root element at the end.
Check the execution result
Let’s check the execution result.
void main(List<String> args) {
print("---- Tree Disjoint Set ----");
final treeDisjointSet = TreeDisJointSet();
run(treeDisjointSet);
final p = treeDisjointSet.findPartition(1);
print("--- merge two times ---");
// 1, 4 are merged in run() func
print(treeDisjointSet.areDisjoint(1, 4)); // false
// 5 is in a different group
print(treeDisjointSet.areDisjoint(1, 5)); // true
print(treeDisjointSet.merge(5, 4)); // true
// 5 is in the same group as 4.
print(treeDisjointSet.areDisjoint(1, 5)); // false
print(treeDisjointSet.merge(2, 4)); // true
treeDisjointSet.show();
// 1: { root: 1, rank: 4 }
// 2: { root: 1, rank: 1 }
// 4: { root: 1, rank: 1 }
// 5: { root: 1, rank: 1 }
// 6: { root: 6, rank: 1 }
// 7: { root: 7, rank: 1 }
}
void run(DisjointSetBase disjointSet) {
disjointSet.add(1);
disjointSet.add(1);
disjointSet.add(2);
disjointSet.add(4);
disjointSet.add(5);
disjointSet.add(6);
disjointSet.add(7);
print("---current disjoint set---");
disjointSet.show();
// 1: { root: 1, rank: 1 }
// 2: { root: 2, rank: 1 }
// 4: { root: 4, rank: 1 }
// 5: { root: 5, rank: 1 }
// 6: { root: 6, rank: 1 }
// 7: { root: 7, rank: 1 }
print(disjointSet.findPartition(1)); // { root: 1, rank: 1 }
print(disjointSet.findPartition(4)); // { root: 4, rank: 1 }
print(disjointSet.areDisjoint(1, 4)); // true
print(disjointSet.merge(1, 4)); // true
print(disjointSet.areDisjoint(1, 4)); // false
print("---current disjoint set---");
disjointSet.show();
// 1: { root: 1, rank: 2 }
// 2: { root: 2, rank: 1 }
// 4: { root: 1, rank: 1 }
// 5: { root: 5, rank: 1 }
// 6: { root: 6, rank: 1 }
// 7: { root: 7, rank: 1 }
}The result in the run() function is almost the same as the naive version. The difference is only the representation of the value.
In the main function, 5 is merged into 4. 4 and 5 are in the same group. 1 and 4 are already merged in run() function, and 1 and 5 are also treated as in the same group.
Application
Let’s simulate shopping in a simple way. A user chooses 3 items from 20 items. It can contain duplicates in the 3 items. If the two items are bought in a row, we merge the two items.
void run2() {
final seed = DateTime.now().millisecond;
final random = Random(seed);
final numberOfItems = 20;
final initialSet = HashMap<int, Tree>.fromIterable(
List.generate(20, (index) => index),
key: (element) => element,
value: (element) => Tree(element),
);
final disjointSet = TreeDisJointSet(initialSet: initialSet);
bool canMerge(List<int> lastValue, int item1, int item2) =>
lastValue.contains(item1) &&
lastValue.contains(item2) &&
disjointSet.areDisjoint(item1, item2);
List<int> lastValue = [];
for (var i = 0; i < 300; i++) {
final item1 = random.nextInt(numberOfItems);
final item2 = random.nextInt(numberOfItems);
final item3 = random.nextInt(numberOfItems);
if (canMerge(lastValue, item1, item2)) {
disjointSet.merge(item1, item2);
}
if (canMerge(lastValue, item1, item3)) {
disjointSet.merge(item1, item3);
}
if (canMerge(lastValue, item2, item2)) {
disjointSet.merge(item2, item3);
}
lastValue = [item1, item2, item3];
}
disjointSet.show();
}This is one of the results.
0: { root: 0, rank: 1 }
1: { root: 14, rank: 1 }
2: { root: 14, rank: 1 }
3: { root: 7, rank: 1 }
4: { root: 6, rank: 1 }
5: { root: 7, rank: 1 }
6: { root: 6, rank: 2 }
7: { root: 7, rank: 3 }
8: { root: 14, rank: 1 }
9: { root: 17, rank: 1 }
10: { root: 10, rank: 1 }
11: { root: 11, rank: 1 }
12: { root: 12, rank: 1 }
13: { root: 13, rank: 1 }
14: { root: 14, rank: 4 }
15: { root: 18, rank: 1 }
16: { root: 17, rank: 1 }
17: { root: 17, rank: 3 }
18: { root: 18, rank: 2 }
19: { root: 19, rank: 1 }Some items are merged. The items that have rank != 1 are merged to the other items.






Comments