This post is the output of this book.
Advanced Algorithms and Data StructuresTreap is Binary Search Tree (BST). It is tree + heap. If you don’t know what Heap is and how it is implemented, check the following post.
Heap has only priority but Treap can have key as well. The priority is sorted in the vertical direction and the key is sorted in the horizontal direction.
The Treap looks like this.
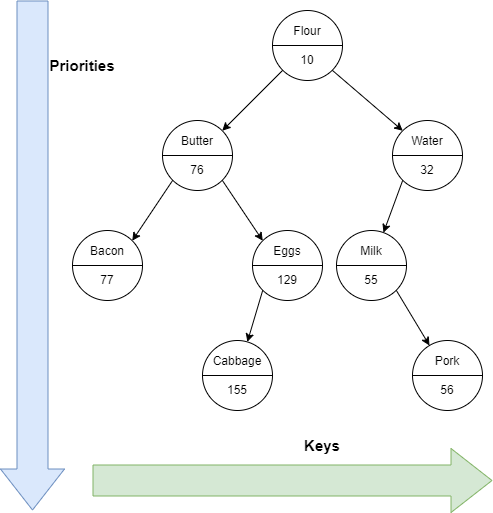
Treap can be a linear tree, which might not be called a tree though, depending on the priority. In this case, the performance gets worse. It’s important to keep the tree balanced for performance. If a random priority is given to an inserted Node, the tree becomes balanced.
So this post explains the implementation of Treap first and then, introduces random priority there.
According to the book, Randomized Treap is often used to implement dictionaries and sets. Randomized Treap would be used everywhere where Binary Search Tree (BST) is used.
In this post, a simple string is used as a key but it is also possible to give a class if it provides a key.
class Product {
public constructor(
private name: string,
private price: number
){ }
public get Key(): string {
return this.name + this.age;
}
// you can provide extra methods/variables
public get PriceWithTax(): number {
...
}
}We could implement a Dictionary class ourselves in this way.
Okay, let’s dive into the implementation detail of Treap! The interface is the following.
interface ITreap {
contains(targetKey: string): boolean;
insert(key: string, priority: number): void;
remove(key: string): boolean;
pop(): string;
peek(): string;
min(): string;
max(): string;
}Node representation
Heap is implemented with Array. By calculating the index number, it is handled as if it is a tree. However, Treap doesn’t use Array. A node has a parent, a left node, and a right node. It has up to 3 node links. We need to implement the class first.
If a node is assigned to the left node, the parent of the added node can also be set. The node needs to be set to undefined or null in another process, so undefined type is also accepted here.
export class Node {
private _left?: Node;
public get Left(): Node | undefined {
return this._left;
}
public set Left(node: Node | undefined) {
this._left = node;
if (node) {
node._parent = this;
}
}
// right node is the same
...
}Node needs to have key and priority. Let’s set them in the constructor.
export class Node {
public constructor(
public readonly Key: string,
public readonly priority: number,
) { }
}The comparison for priority is done in Treap class but it needs to give a way to compare the key in this class.
The expected result is the following.
| Node key | targetKey | Result |
|---|---|---|
| aBc | Acc | false |
| Acc | aBc | true |
| AAAA | AAA | true |
| AAA | AAA | true |
export class Node {
public biggerThan(targetKey: string): boolean {
for (let i = 0; i < this.Key.length; i++) {
const original = this.Key[i].toLowerCase();
const target = targetKey[i]?.toLowerCase();
if (original === target) {
continue;
}
if (target === undefined) {
// original key is longer than target
return true;
}
return original > target;
}
// same key or targetKey is longer
return this.Key.length >= targetKey.length;
}
}The complete implementation of Node class is the following.
export class Node {
private _left?: Node;
public get Left(): Node | undefined {
return this._left;
}
public set Left(node: Node | undefined) {
this._left = node;
if (node) {
node._parent = this;
}
}
private _right?: Node;
public get Right(): Node | undefined {
return this._right;
}
public set Right(node: Node | undefined) {
this._right = node;
if (node) {
node._parent = this;
}
}
private _parent?: Node;
public get Parent(): Node | undefined {
return this._parent;
}
public set Parent(node: Node | undefined) {
this._parent = node;
}
public constructor(
public readonly Key: string,
public readonly priority: number,
) { }
public biggerThan(targetKey: string): boolean {
for (let i = 0; i < this.Key.length; i++) {
const original = this.Key[i].toLowerCase();
const target = targetKey[i]?.toLowerCase();
if (original === target) {
continue;
}
if (target === undefined) {
// original key is longer than target
return true;
}
return original > target;
}
// same key or targetKey is longer
return this.Key.length >= targetKey.length;
}
}Rotation
When it’s heap, it just swaps the two nodes if the two nodes violate the rule. Treap is not so simple because it needs to care for both priority and key. The rotation is used when inserting and removing a node to keep the tree state.
The behavior is the following.
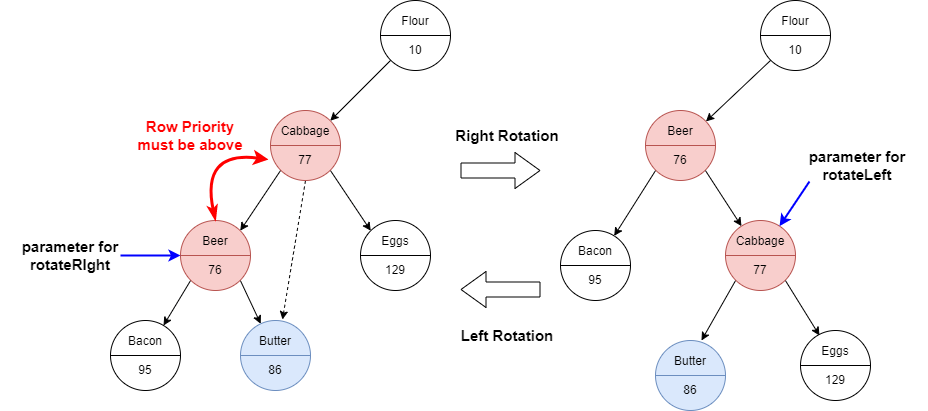
The target node Beer needs to be one level above. So, the child node of the parent of parent needs to be linked to Beer node. Then, cabbage must be a child node of Beer. In addition to that, the child node of Beer node somehow needs to be linked somewhere. The order of the keys are
Beer -> Butter -> Cabbage
therefore, it needs to be the left node of the Cabbage node.
The code becomes looks like this.
export class Treap implements ITreap{
private root?: Node;
// this should be private
// this is for writing test
protected rotateRight(target: Node): void {
if (!this.hasParent(target)) {
throw new Error("Specified node is a root node")
}
const parent = target.Parent;
if (parent.Left != target) {
throw new Error("Right rotation can be performed only on a left node.");
}
const parentOfParent = parent.Parent;
if (parentOfParent) {
if (parentOfParent.Left === parent) {
parentOfParent.Left = target;
} else {
parentOfParent.Right = target;
}
} else {
this.root = target;
this.root.Parent = undefined;
}
parent.Left = target.Right;
target.Right = parent
}
}The implementation of the rotateLeft is almost the same as rotateRight.
export class Treap implements ITreap {
protected rotateLeft(target: Node): void {
if (!this.hasParent(target)) {
throw new Error("Specified node is a root node")
}
const parent = target.Parent;
if (parent.Right !== target) {
throw new Error("Left rotation can be performed only on a Right node.");
}
const parentOfParent = parent.Parent;
if (parentOfParent) {
if (parentOfParent.Left === parent) {
parentOfParent.Left = target;
} else {
parentOfParent.Right = target;
}
} else {
this.root = target;
this.root.Parent = undefined;
}
parent.Right = target.Left;
target.Left = parent;
}
}Insert
To insert a node, the new node needs to be placed at one of the leaves. If it violates the state, it calls rotation method until the state becomes good.
The first part is to look for the leaf node. The two keys need to be compared. It goes to the right node if the new key is bigger than the original node’s key. Otherwise, left node.
export class Treap implements ITreap {
public insert(key: string, priority: number): void {
let node = this.root;
let parent: Node | undefined;
const newNode = new Node(key, priority);
// Search for a parent leaf
while (node) {
parent = node;
if (node.biggerThan(key)) {
node = node.Right;
} else {
node = node.Left;
}
}
...
}
}Once the parent node for the new node is found, we can add the new node there. The new node needs to be added to the left node if the new key is smaller than the parent’s key. Then, set the parent node to the parent of the new node.
export class Treap implements ITreap {
public insert(key: string, priority: number): void {
...
// Add the new node as a leaf
if (!parent) {
this.root = newNode;
return;
} else if (parent.biggerThan(key)) {
parent.Left = newNode;
} else {
parent.Right = newNode;
}
newNode.Parent = parent;
...
}
}We looked for a leaf node depending on the key but the priority is not considered here. So, it is likely not sorted in terms of the priority value.
Compare the priority with the parent and the new node. If it violates the rule, call rotation method until the tree state becomes good.
export class Treap implements ITreap {
public insert(key: string, priority: number): void {
...
// Fix the priority violations
while (newNode.Parent && newNode.priority < newNode.Parent.priority) {
if (newNode == newNode.Parent.Left) {
this.rotateRight(newNode);
} else {
this.rotateLeft(newNode);
}
}
if (!newNode.Parent) {
this.root = newNode;
}
}
}The whole code looks like this.
export class Treap implements ITreap {
public insert(key: string, priority: number): void {
let node = this.root;
let parent: Node | undefined;
const newNode = new Node(key, priority);
// Search for a parent leaf
while (node) {
parent = node;
if (node.biggerThan(key)) {
node = node.Left;
} else {
node = node.Right;
}
}
// Add the new node as a leaf
if (!parent) {
this.root = newNode;
return;
} else if (parent.biggerThan(key)) {
parent.Left = newNode;
} else {
parent.Right = newNode;
}
newNode.Parent = parent;
// Fix the priority violations
while (newNode.Parent && newNode.priority < newNode.Parent.priority) {
if (newNode == newNode.Parent.Left) {
this.rotateRight(newNode);
} else {
this.rotateLeft(newNode);
}
}
if (!newNode.Parent) {
this.root = newNode;
}
}
}Search and Contains
Search method is easier than insert. Compare the two keys and go to left or right, until the same key is found. It means that the method needs to be called recursively.
Contains method just checks if the result of search call is not undefined.
export class Treap implements ITreap {
// it's protected for writing test
protected search(targetKey: string): Node | undefined {
const recursive = (node: Node | undefined, targetKey: string): Node | undefined => {
if (!node) {
return undefined;
}
if (node.Key == targetKey) {
return node;
} else if (node.biggerThan(targetKey)) {
return recursive(node.Left, targetKey);
}
return recursive(node.Right, targetKey);
}
return recursive(this.root, targetKey);
}
public contains(targetKey: string): boolean {
return !!this.search(targetKey);
}
}Delete
To delete the target node, the target key must be searched first. If it’s not found, it doesn’t delete anything of course. If the target node is a root node and the node doesn’t have any child node, we can just set undefined to the root. This is the code for this part.
type HasParentNode = Node & { Parent: Node };
export class Treap implements ITreap {
public remove(key: string): boolean {
const node = this.search(key);
if (!node) {
return false;
}
if (!this.hasParent(node) && this.isLeaf(node)) {
this.root = undefined;
return true;
}
...
}
/**
* Node is a root if this function returns false.
* @param node
* @returns
*/
private hasParent(node: Node): node is HasParentNode {
return !!node.Parent;
}
private isLeaf(node: Node): boolean {
return !node.Left && !node.Right;
}
}If the node doesn’t have a parent node, it’s a root node. I defined HasParentNode type to let IntelliSense know that parent of the node is not undefined in the following code.
Okay, let’s go forward. If the removed node has children, we put a node that has higher priority to the removed node position. If the left child priority is bigger than right node, call rotateRight.
It means that the removed node goes one level down. This process needs to be repeated until the removed node reaches a leaf. Once the node becomes a leaf, the parent node of the removed node needs to delete the connection to the removed node.
type HasParentNode = Node & { Parent: Node };
export class Treap implements ITreap {
public remove(key: string): boolean {
const node = this.search(key);
if (!node) {
return false;
}
if (!this.hasParent(node) && this.isLeaf(node)) {
this.root = undefined;
return true;
}
while (!this.isLeaf(node)) {
if (node.Left && (!node.Right || node.Left.priority > node.Right.priority)) {
this.rotateRight(node.Left);
} else if (node.Right) {
this.rotateLeft(node.Right)
}
if (node.Parent && !this.hasParent(node.Parent)) {
this.root = node.Parent;
}
}
// the node became a leaf here. Parent must exist.
if (!node.Parent!.Left) {
node.Parent!.Left = undefined;
} else {
node.Parent!.Right = undefined;
}
return true;
}
/**
* Node is a root if this function returns false.
* @param node
* @returns
*/
private hasParent(node: Node): node is HasParentNode {
return !!node.Parent;
}
private isLeaf(node: Node): boolean {
return !node.Left && !node.Right;
}
}Pop, peek, Min, and Max
It’s not necessary to explain about peek to get the root key. Pop method needs to remove the root node. Therefore, it needs to call remove method in it. Rotation is done under the hood to keep the tree state.
export class Treap implements ITreap {
public pop(): string {
if (!this.root) {
throw new Error("Treap is empty");
}
const key = this.root.Key;
this.remove(key);
return key;
}
public peek(): string {
if (!this.root) {
throw new Error("Treap is empty");
}
return this.root.Key;
}
}Last, min and max. The minimum value is on the left side while the maximum is on the right side. Then, go to the direction until undefined is found.
export class Treap implements ITreap {
public min(): string {
if (!this.root) {
throw new Error("Treap is empty");
}
let node = this.root;
while (node.Left) {
node = node.Left;
}
return node.Key;
}
public max(): string {
if (!this.root) {
throw new Error("Treap is empty");
}
let node = this.root;
while (node.Right) {
node = node.Right;
}
return node.Key;
}
}Randomized Treap
The implementation is almost the same. The difference is only the insert method. Generate a random value and give it as priority. The internal implementation is the same as Treap.
this.treap.insert(key, Math.random());So the whole code looks like the following.
import { Node } from "./Node";
import { Treap } from "./Treap";
export class RandomizedTreap {
private treap: Treap;
public constructor() {
this.treap = new Treap();
}
public search(targetKey: string): Node | undefined {
return this.treap.search(targetKey);
}
public insert(key: string): void {
this.treap.insert(key, Math.random());
}
public remove(key: string): boolean {
return this.treap.remove(key);
}
public pop(): string {
return this.treap.pop();
}
public peek(): string {
return this.treap.peek();
}
public min(): string {
return this.treap.min();
}
public max(): string {
return this.treap.max();
}
}The class doesn’t extend Treap because the representation of the insert method is different. Treap insert method requires priority but the Randomized Treap insert doesn’t require it. extends keyword should not be used for this reason.
Go to my repository if you want to check the complete code. I wrote unit tests for some methods.
If you are interested in data structure, I highly recommend this book. It has over 700 pages!
Advanced Algorithms and Data Structures




Comments